Heat Capacity

For a gas of molecular weight $M$ specific heat capacity at constant pressure is $\left(r=\frac{c_p}{c_v}\right)$

Why the specific heat at a constant pressure is more than that at constant volume.

What is specific heat of gas at constant pressure

At a given temperature, the specific heat of a gas at constant pressure is always greater than its specific heat at constant volume.

$C_p-C_v=\frac{R}{M}$ and $C_v$ are specific heats at constant pressure and constant volume respectively. It is observed that, $C_p-C_v=a$ for hydrogen gas and $C_p-C_v=b$ for nitrogen gas. The correct relation between $a$ and $b$ is:

Assertion: The specific heat at constant pressure is greater than the specific heat at constant volume i.e., $C_P > C_V$ .

Reason: In case of specific heat at constant volume, the whole of heat supplied is used to raise the temperature of one mole of the gas through $1°C$ while in case of specific of heat at constant pressure, heat is to be supplied not only for heating 1 mole of gas through $1°C$ but also for doing work during expansion of the gas.

An engine takes in $5$ moles of air at $20 °\mathrm{C}$ and $1 \mathrm{atm},$ and compresses it adiabatically to ${\left(\frac{1}{10}\right)}^{th}$ of the original volume. Assuming air to be a diatomic ideal gas made up of rigid molecules, the change in its internal energy during this process comes out to be $x \mathrm{kJ}$. The value of $x$ to the nearest integer is

The ratio of translational and rotational kinetic energies for $1$ mole gas at $200 K$ temperature is $3: 2 .$ The internal energy of one mole gas at that temperature is $x\times {10}^2 \mathrm{J}.$ Then value of $x$ is $[R=8.3 J/mol-K]$

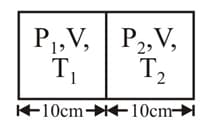
An insulating container of gas has $2$ chambers separated by insulating partition. Initially both chambers has equal volume of same gas. Temperature and pressure of left chamber is $T_1$ and $P_1$ and for right chamber is $T_2$ and $P_2.$ Now partition is moved towards right by $5 \mathrm{cm}$ maintaining constant pressure on both sides as earlier and after some time partition is removed without doing any work on gas. If final temperature of gas is $\frac{\alpha {\mathrm{P}}_1+\beta {\mathrm{P}}_2}{\frac{{\mathrm{P}}_1}{{ \mathrm{T}}_1}+\frac{{\mathrm{P}}_2}{{ \mathrm{T}}_2}}$ find $\alpha +\beta$

1 mole of a monoatomic ideal gas and 3 mole of a diatomic ideal gas are mixed. If both gasses can not react then what will be $\mathrm{\gamma }=\frac{{\mathrm{C}}_{\mathrm{p}}}{{\mathrm{C}}_{\mathrm{v}}}$ for mixture ? (${\mathrm{C}}_{\mathrm{p}}$ and ${\mathrm{C}}_{\mathrm{v}}$ are molar specific heat capacities)

An insulated box containing a diatomic gas of molar mass $M$ is moving with velocity $v$. The box is suddenly stopped. The resulting change in temperature is $\frac{m{v}^2}{fR}$. What will be the value of $f$?

If ${\mathrm{S}}_{\mathrm{P}}$ and ${\mathrm{S}}_{\mathrm{V}}$ denote the specific heats of nitrogen gas per unit mass at constant pressure and constant volume respectively, then

The ratio of the molar heat capacities of a diatomic gas at constant pressure to that at constant volume is

A molecule of a gas has six degrees of freedom. Then, the molar specific heat of the gas at constant volume is

One gram mole of an ideal gas $A$ with the ratio of constant pressure and constant volume specific heats ${\gamma }_A=\frac{5}{3}$ is mixed with $n$ gram moles of another ideal gas $B$ with ${\gamma }_B=\frac{7}{5}$. If the $\gamma$ for the mixture is $\frac{19}{13}$, then what will be the value of $n$?

A rigid triangular molecule consists $8$ degrees of freedom. The adiabatic constant $\left(\gamma =\frac{C_p}{C_v}\right)$ of an ideal gas consisting of such molecules is

Specific heat of an ideal gas at constant volume $C_v$ and at constant pressure $C_p$ are related to universal gas constant are as

 One mole of $\mathrm{a}$ an ideal gas is heated at constant pressure through $1\mathrm{K}$work done by the gas is

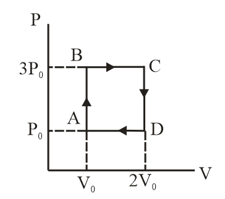
An ideal monatomic gas is carried along the cycle $ABCDA$ as shown in the figure. The total heat absorbed in this process is

A gaseous mixture consists of $16 \mathrm{g}$ of helium and $16 \mathrm{g}$ of oxygen. The ratio $\left(C_p/C_v\right)$ of the mixture is